Lab 8: MCMC Algorithms and Considerations

For the class on Wednesday, February 7th

Tip

In this lab, questions are embedded in the implementation steps, but are always shown in bold. Don’t forget to answer the questions.

The following cell defines the same IsingModel2D class that we introduced in Lab 7.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

class IsingModel2D:
    def __init__(self, side_size: int, boundaries=None, initial_values="cold", antiferro=False):
        self._side_size = int(side_size)
        self._size = self._side_size * self._side_size

        indices = np.arange(self._size).reshape((self._side_size, self._side_size))
        neighbor_indices = np.stack([
            np.roll(indices, 1, 0),   # up
            np.roll(indices, -1, 1),  # right
            np.roll(indices, -1, 0),  # down
            np.roll(indices, 1, 1),   # left
        ])

        if boundaries not in [None, "periodic"]:
            try:
                bu, br, bd, bl = boundaries
            except TypeError:
                bu = br = bd = bl = boundaries
            idx = np.arange(self._size, self._size + 3)
            for bv, s in zip([bu, br, bd, bl], [(0,0), (1,Ellipsis,-1), (2,-1), (3,Ellipsis,0)]):
                neighbor_indices[s] = idx[int(np.sign(bv))]

        self._neighbor_indices = neighbor_indices.reshape(4, self._size).T

        self._data = np.empty(self._size + 3, dtype=np.int32)
        self._data[-3:] = [0, 1, -1]
        if isinstance(initial_values, str):
            if initial_values == "hot":
                self.data = np.random.default_rng().random(self._size) >= 0.5
            elif initial_values == "cold":
                self.data = 1
        else:
            self.data = initial_values

        self._J = float(-1 if antiferro else 1)

    @property
    def size(self):
        return self._size

    @property
    def data(self):
        return self._data[:-3].reshape(self._side_size, self._side_size).copy()

    @data.setter
    def data(self, value):
        value = np.ravel(value)
        if len(value) not in [1, self._size]:
            raise ValueError(f"`value` must be a single value or an array of size {self._size}")
        new_value = np.ones(len(value), dtype=np.int32)
        new_value[~(value > 0)] = -1
        if len(new_value) == 1:
            new_value = new_value[0]
        self._data[:-3] = new_value

    def show(self, **kwargs):
        plt.matshow(self.data, vmax=1, vmin=-1, **kwargs)

    def _check_site_index(self, site_index: int):
        if not isinstance(site_index, int):
            i, j = site_index
            site_index = int(i) * self._side_size + int(j)
        if site_index >= 0 and site_index < self._size:
            return site_index
        raise ValueError(f"`site_index` must be between 0 and {self._size - 1} (inclusive)")

    def calc_magnetization(self):
        return self._data[:self._size].sum(dtype=np.float64) / self._size

    def calc_total_energy(self, ext_field=0.0):
        energy = (
            self._data[self._neighbor_indices].sum(axis=1, dtype=np.float64)
            * self._data[:self._size]
        ).sum(dtype=np.float64) * self._J * (-0.5)
        if ext_field:
            energy -= self._data[:self._size].sum(dtype=np.float64) * float(ext_field)
        return energy

    def calc_local_energy(self, site_index: int, ext_field=0.0):
        site_index = self._check_site_index(site_index)
        energy = (
            self._data[self._neighbor_indices[site_index]].sum(dtype=np.float64)
            * self._data[site_index]
            * self._J
            * (-1.0)
        )
        if ext_field:
            energy -= self._data[site_index] * float(ext_field)
        return energy

    def flip(self, site_index):
        self._data[self._check_site_index(site_index)] *= -1

    def transition_prob_metropolis(self, site_index: int, beta: float, ext_field=0.0):
        return np.exp(2.0 * beta * self.calc_local_energy(site_index, ext_field))

    def transition_prob_gibbs(self, site_index: int, beta: float, ext_field=0.0):
        return 1.0 / (1.0 + np.exp(-2.0 * beta * self.calc_local_energy(site_index, ext_field)))

    def sweep(self, beta, ext_field=0.0, nsweeps=1, seed=None, transition_prob="metropolis"):
        rng = np.random.default_rng(seed)
        transition_prob_func = getattr(self, f"transition_prob_{transition_prob}")
        accept = 0
        for _  in range(nsweeps):
            for i in range(self._size):
                if rng.random() < transition_prob_func(i, beta, ext_field):
                    self.flip(i)
                    accept += 1
        return accept / self._size / nsweeps

A. Metropolis-Hastings vs. Gibbs Sampling Methods

If we start a 2D Ising model with the “cold” initial condition, and set \(\beta\) to a value lower than the critical value (corresponding to a temperature higher than the critical temperature, the Metropolis-Hastings algorithm could fail if the value of \(\beta\) is too low.

1. In the code cell below, try a few difference small values of \(\beta\) and describe what you observe. Specifically, how do the value of \(\beta\), the acceptance rate, and the resulting lattice relate to each other? Make some plots to demonstrate your answer.

2. Repeat Step 1 but use the Gibbs sampling method by setting transition_prob='gibbs' when calling the sweep method. Describe what you observe.

---

// Write your answers to Part A here

---

# Here's the starting point for Step 1

m = IsingModel2D(25, initial_values="cold")
beta = 0.2
acceptance = m.sweep(beta, nsweeps=50)
print(acceptance)
m.show()

0.69376

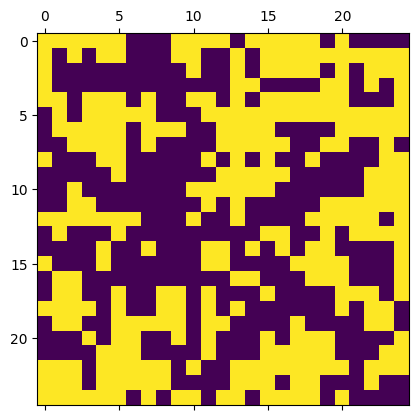
# Include your implementation for Part A here

B. Time to Equilibrate (Burn-in)

1. Set up a 30-by-30 lattice with the “hot” initial condition.

2. Set beta to 0.55.

3. Run sweep 1,000 times, but each time with nsweeps=1. After each run, record the average magnetization.

4. Make a plot of average magnetization as a function of number of sweeps have run.

5. Describe what you observe. Does the magnetization reach a plateau? How long does it take to reach a plateau?

6. Repeat [Steps 1-4] but with beta set to 0.45.

---

// Write your answers to Part B here

---

# Include your implementation for Part B here

C. Autocorrelation

1. Set up a 30-by-30 lattice with the “hot” initial condition.

2. Set beta to 0.45.

3. Run sweep 1,000 times, but each time with nsweeps=1. After first 100 sweeps, start to record the average magnetization.

4. Calculate the average of the 900 average magnetization. We’ll call this \(\langle m \rangle_c\).

5. Subtract \(\langle m \rangle_c\) from the 900 magnetization you collected.

6. Calculate the autocorrelation of magnetization (with average subtracted) using the autocorr function (defined below)

7. Describe what you observe. Does the autocorrelation deacys? How fast does it decay?

8. Repeat [Steps 1-7] but with beta set to 0.55.

---

// Write your answers to Part C here

---

def autocorr(x):
    result = np.correlate(x, x, mode='full')
    return result[result.size // 2:]

# Include your implementation for Part C here

Final question

Roughly how much time did you spend on this lab (not including the time you spent in class)?

---

// Write your answers here

---

Tip

How to submit this notebook on Canvas?

Once you complete this lab and have all your code, text answers, and all the desired results after running the notebook properly displayed in this notebook, please convert the notebook into HTML format by running the following:

jupyter nbconvert --to html /path/to/labs/08.ipynb 

Then, upload the resulting HTML file to Canvas for the corresponding assignment.